Poker 4 Of A Kind Vs Straight Flush
Royal Flush
Four-of-a-Kind Aces will always bear 4-of-a-Kind Kings, and Quad Kings will always beat Quad Queens, and so forth. How Does a 4-of-a-Kind Hand Match Up? Four-of-a-Kind is the second best possible hand in the poker hand ranking system. Only a Straight Flush ranks above it.
Ace high Straight Flush.
Ace of Spades King of Spades Queen of Spades Jack of Spades 10 of Spades in a single suit. Also frequently referred to as 'Broadway'.
Straight Flush
Five consecutive cards of the same suit.
- If two or more players share the same four of a kind, then the fifth card kicker determines the winner. Straight Flush: A straight flush (five consecutive cards all of the same suit) beats four of a kind. Aces can be high or low. An ace-high straight flush is called a royal flush, the best possible hand in poker.
- 10 (straight flushes per suit).4(total suits)= 40 straight flush 5-card hand combinations 13 (four of a kind combinations). (12 the kicker) = 156 5-card poker hand combinations Therefore 40.
- A hand that consists of three cards of the same suit in consecutive ranking. King, queen and jack are the highest ranked straight flush and ace, 2 and 3 is the lowest ranked straight flush. Three of a Kind: A hand that consists of three cards of the same rank. Three aces is the highest ranked three of a kind and three 2’s is the.
Five sequential cards in the same suit. The highest type of Straight Flush is a Royal Flush, and the lowest is an A-2-3-4-5 hand (if Aces are low or high/low). This type of hand is referred to as a 'Steel Wheel'. Other Straight Flushes with special names include:
- King of Clubs Queen of Clubs Jack of Clubs 10 of Clubs 9 of Clubs - Off Broadway (because it's shifted down one rank from a Royal Flush, or 'Broadway').
Four of a Kind
One of each suit in a single rank.
Also known as Quads. Many of the Four of a Kind hands have their own nicknames:
- King of Clubs King of Diamonds King of Hearts King of Spades - Four Horsemen (of the Apocalypse)
- Queen of Clubs Queen of Diamonds Queen of Hearts Queen of Spades - Village People (four Queens)
- 10 of Clubs 10 of Diamonds 10 of Hearts 10 of Spades - Larry, after Larry Fortensky (four-ten-sky), Elizabeth Taylor's eighth husband
- 4 of Clubs 4 of Diamonds 4 of Hearts 4 of Spades - Yacht Club (because the 4 resembles a sail)
- 3 of Clubs 3 of Diamonds 3 of Hearts 3 of Spades - Forest (four 'trees')
- 2 of Clubs 2 of Diamonds 2 of Hearts 2 of Spades - Mighty Ducks (because the 2 resembles a duck)
Full House
Three of a Kind and One Pair.
A Full House is called as 'X over Y' where X is the Three of a Kind and Y is the Pair (e.g., in a A-A-A-Q-Q hand, you would call it as 'Full House, Aces over Queens').
A Full House is sometimes called a boat or a full boat. When called a Boat/Full Boat, the hand is announced as 'X full of Y' (e.g., the same A-A-A-Q-Q hand would be called a 'Full Boat, Aces full of Queens'). Some Full House hands have special nicknames:
- Ace of Clubs Ace of Diamonds 2 of Clubs 2 of Diamonds 2 of Hearts - Marksman (bows and arrows)
- 7 of Clubs 7 of Diamonds 7 of Clubs 4 of Diamonds 4 of Hearts - Sailing rednecks
- 3 of Clubs 3 of Diamonds 3 of Clubs 2 of Diamonds 2 of Hearts - Nits and Lice, Mites and Lice
Flush
Five cards of the same suit.
Any five cards, all of which are in the same suit. A Flush all in hearts is referred to as 'Valentine's' while a flush all in clubs is known as a 'Golf Bag'.
Straight
Five consecutive cards.
Five cards in sequential order (but not all in the same suit, or it would be a Straight Flush). Also known as a Run (in many melding/counting games, such as gin and its variants, cribbage, and canasta, a Straight is referred to as a Run, and the name has carried over into poker).
- 6 of Clubs 5 of Diamonds 4 of Hearts 3 of Spades 2 of Clubs - Rabbit (the lowest Straight Flush if Aces are high)
- 5 of Clubs 4 of Diamonds 3 of Hearts 2 of Spades Ace of Clubs - Wheel, Bicycle, Bike, Spike, First Street, Little Wheel (the lowest run if Aces are low or high/low)
Three of a Kind
Three cards of the same rank. Also known as Trips, a Set, or Triplets. Three-card combinations that have special names include:
- Ace of Clubs Ace of Diamonds Ace of Hearts - Beatles reunion
- King of Clubs King of Diamonds King of Hearts - Three Wise Men, Christmas Special (both references to 'Three Kings'), Alabama Night Riders, Ku Klux Klan (KKK is an abbreviation for the Ku Klux Klan, and 'Alabama Night Riders' is a colloquial term used to refer to this group, which has a history of carrying out their acts at night in rural ateas)
- Queen of Clubs Queen of Diamonds Queen of Hearts - Six Tits
- Jack of Clubs Jack of Diamonds Jack of Hearts - Hart, Schaffner, and Marx (Three Jacks)
- 10 of Clubs 10 of Diamonds 10 of Hearts - Dallas to Fort Worth (the I-10 connects these two Texas Cities), San Jose to Gilroy, Gilroy, Thirty Miles of bad road (the distance between San Jose and Gilroy, California, used to be 30 miles, although the two cities are now adjoining)
- 7 of Clubs 7 of Diamonds 7 of Hearts - 21, Slot Machine, Jackpot (all named after results in other casino games like Blackjack and Slots)
- 6 of Clubs 6 of Diamonds 6 of Hearts - The Devil, The Beast, Lucifer, Devil's Area Code
- 5 of Clubs 5 of Diamonds 5 of Hearts - Washington Monument, Pork Chop Sandwiches
- 4 of Clubs 4 of Diamonds 4 of Hearts - Grand Jury
- 2 of Clubs 2 of Diamonds 2 of Hearts - Huey, Dewey, and Louie (three ducks)
Two Pairs
Two pairs, each with two cards of the same rank. Notable named two pair combinations include:
- Ace of Clubs Ace of Diamonds 8 of Clubs 8 of Diamonds - Dead Man's Hand (Arrows and Nooses)
- King of Clubs King of Diamonds Queen of Clubs Queen of Diamonds - Mommas and Poppas
- King of Clubs King of Diamonds 9 of Clubs 9 of Diamonds - Pair of Dogs (because it's K9K9-- two canines)
- Queen of Clubs Queen of Diamonds 3 of Clubs 3 of Diamonds - San Francisco Waiters (Queens with Trays/Treys)
- Jack of Clubs Jack of Diamonds 5 of Clubs 5 of Diamonds - Jackson Five (Jacks and Fives), Motown, Rock and Roll
- Jack of Clubs Jack of Diamonds 3 of Clubs 3 of Diamonds - Hookers with Crabs (because the Jacks hook and the 3 is like a sideways crab)
- 9 of Clubs 9 of Diamonds 8 of Clubs 8 of Diamonds - Oldsmobile
- 9 of Clubs 9 of Diamonds 6 of Clubs 6 of Diamonds - Dinner for Four
- 3 of Clubs 3 of Diamonds 2 of Clubs 2 of Diamonds - Socks and Shoes, Mites and Lice, Mits and Mites, Nits and Lice
One Pair
Two cards of the same rank. The poker hand that contains a single pair that is the most worth noting is the Princess Leia (an A-A-2-3), so called because the room in which Leia was imprisoned in Star Wars was room A-A-2-3. The best known names given to (pocket) pairs include:
- Ace of Clubs Ace of Diamonds - Pocket Rockets, Bullets, American Airlines
- King of Clubs King of Diamonds - Cowboys, King Kong
- Queen of Clubs Queen of Diamonds - Bitches, Double date, Canadian Aces, Siegfried and Roy
- Jack of Clubs Jack of Diamonds - Fish Hooks
- 9 of Clubs 9 of Diamonds - German Virgin (no, we don't know why.)
- 8 of Clubs 8 of Diamonds - Snowmen
- 7 of Clubs 7 of Diamonds - Sunset Strip, Hockey Sticks
- 6 of Clubs 6 of Diamonds - Route 66
- 5 of Clubs 5 of Diamonds - Speed limit
- 4 of Clubs 4 of Diamonds - Magnum, Sail Boat
- 3 of Clubs 3 of Diamonds - Crabs
- 2 of Clubs 2 of Diamonds - Ducks
High Card
While the high card is the lowest possible hand in poker (every poker hand automatically has a 'high card' in it-- the card with the greatest value), it comes into play in some poker variants more than others. Poker rookies often underestimate the value of the high card.
Texas Hold'em, for instance, is frequently referred to as a game of high cards because a player with higher cards always has an advantage. If player 1 holds K-Q and player 2 holds J-10, there are three possible outcomes:
- The flop makes player 1's hand, and player 1 wins.
- The flop makes player 2's hand, and player 2 wins.
- The flop doesn't make either player's hand, and player 1 wins again.
The player with high cards has a statistical advantage and will win 63% of the time.
Well known nicknames given to pocket hands are:
- Ace of Clubs King of Diamonds - Big Slick, Anna Kournikova (looks great, never wins!)
- Ace of Clubs Queen of Diamonds - Big Chick
- Ace of Clubs Jack of Diamonds - Black Jack, Jack-Ass
- King of Clubs Queen of Diamonds - Royalty, Marriage
- King of Clubs Jack of Diamonds - Kojak
- Jack of Clubs 5 of Diamonds - Jackson Five
- Queen of Clubs 3 of Diamonds - Gay Waiter
- 9 of Clubs 5 of Diamonds - Dolly Parton
- Ace of Clubs 8 of Diamonds - Dead Man's Hand (player Wild Bill Hickok was shot in 1876 after winning with it!)
- King of Clubs 9 of Diamonds - Canine
- Jack of Clubs 4 of Diamonds - Flat Tire
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
___________________________________________________________________________
Preliminary Calculation
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
Poker Straight Flush Vs 4 Of Kind
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced “n choose r”, which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.

Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
Poker 4 Of A Kind Vs Straight Flush Machine
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of “3 diamond, 2 heart” hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
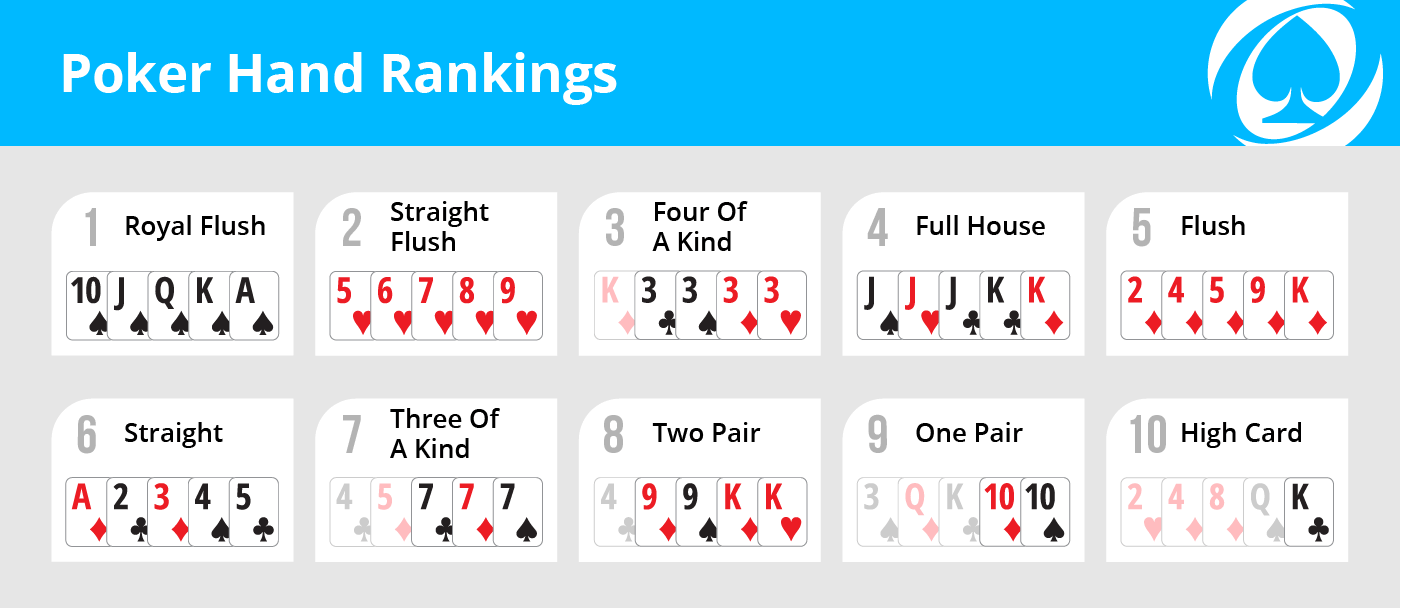
Here’s a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let’s fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2’s and choosing 2 cards out of the four 8’s. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.

Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.
High Card
The count is the complement that makes up 2,598,960.
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Poker 4 Of A Kind Vs Straight Flush Toilets
Probabilities of Poker Hands
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
Poker 4 Of A Kind Vs Straight Flush Toilet
___________________________________________________________________________
2017 – Dan Ma